Electron. J. Diff. Eqns.,Vol. 2004(2004), No. 132, pp. 1-15.
Existence and multiplicity of positive solutions
for a singular problem associated to the p-Laplacian operator
Carlos Aranda, Tomas Godoy
Abstract:
Consider the problem
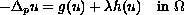
with
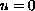 on the boundary, where
on the boundary, where
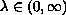 ,
,
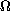 is a strictly convex bounded and
is a strictly convex bounded and
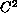 domain in
domain in
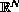 with
with
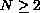 , and
, and
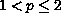 .
Under suitable assumptions on
.
Under suitable assumptions on
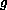 and
and
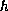 that allow a singularity of
that allow a singularity of
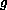 at the origin, we show that for
at the origin, we show that for
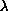 positive and small enough the above problem has at least
two positive solutions in
positive and small enough the above problem has at least
two positive solutions in
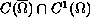 and that
and that
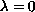 is a bifurcation point from infinity.
The existence of positive solutions for problems of the form
is a bifurcation point from infinity.
The existence of positive solutions for problems of the form
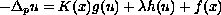 in
in
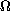 ,
,
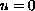 on
on
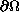 is also studied.
is also studied.
Submitted June 18, 2004. Published November 16, 2004.
Math Subject Classifications: 35J60, 35J65.
Key Words: Singular problems; p-laplacian operator;
nonlinear eigenvalue problems.
Show me the
PDF file (292K),
TEX file for this article.
 |
Carlos Aranda
Departamento de Matematica de la Facultad de Ciencias
Universidad de Tarapaca
Av. General Velasquez 1775
Casilla 7-D, Arica, Chile
email: caranda@uta.cl |
|---|
| |
Tomas Godoy
FaMAF, Universidad Nacional de Cordoba
Medina Allende y Haya de la Torre
Ciudad Universitaria, 5000 Cordoba, Argentina
email: godoy@mate.uncor.edu |
Return to the EJDE web page
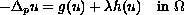
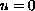 on the boundary, where
on the boundary, where
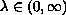 ,
,
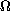 is a strictly convex bounded and
is a strictly convex bounded and
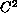 domain in
domain in
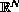 with
with
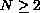 , and
, and
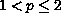 .
Under suitable assumptions on
.
Under suitable assumptions on
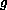 and
and
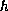 that allow a singularity of
that allow a singularity of
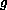 at the origin, we show that for
at the origin, we show that for
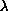 positive and small enough the above problem has at least
two positive solutions in
positive and small enough the above problem has at least
two positive solutions in
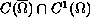 and that
and that
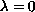 is a bifurcation point from infinity.
The existence of positive solutions for problems of the form
is a bifurcation point from infinity.
The existence of positive solutions for problems of the form
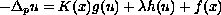 in
in
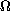 ,
,
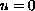 on
on
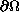 is also studied.
is also studied.
