Electron. J. Diff. Eqns., Vol. 2004(2004), No. 133, pp. 1-8.
Positive solutions for singular semi-positone Neumann
boundary-value problems
Yong-Ping Sun, Yan Sun
Abstract:
In this paper, we study the singular semi-positone Neumann
bound\-ary-value problem
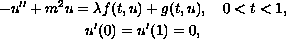
where
 is a positive constant.
Under some suitable assumptions on the functions
is a positive constant.
Under some suitable assumptions on the functions
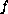 and
and
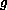 ,
for sufficiently small
,
for sufficiently small
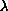 ,
we prove the existence of a
positive solution. Our approach is based on the Krasnasel'skii
fixed point theorem in cones.
,
we prove the existence of a
positive solution. Our approach is based on the Krasnasel'skii
fixed point theorem in cones.
Submitted October 12, 2004. Published November 16, 2004.
Math Subject Classifications: 34B10, 34B15.
Key Words: Positive solution; semi-positone; fixed points; cone;
singular Neumann boundary-value problem.
Show me the
PDF file (189K),
TEX file for this article.
 |
Yong-Ping Sun
Department of Mathematics, Qufu Normal University
Qufu, Shandong 273165, China.
Department of Fundamental Courses
Hangzhou Radio & TV University
Hangzhou, Zhejiang 310012, China
email: syp@mail.hzrtvu.edu.cn |
|---|
 |
Yan Sun
Department of Mathematics
Qufu Normal University
Qufu, Shandong 273165, China
email: ysun@163169.net
|
|---|
Return to the EJDE web page
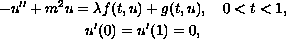
 is a positive constant.
Under some suitable assumptions on the functions
is a positive constant.
Under some suitable assumptions on the functions
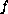 and
and
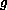 ,
for sufficiently small
,
for sufficiently small
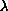 ,
we prove the existence of a
positive solution. Our approach is based on the Krasnasel'skii
fixed point theorem in cones.
,
we prove the existence of a
positive solution. Our approach is based on the Krasnasel'skii
fixed point theorem in cones.

