Electron. J. Diff. Eqns., Vol. 2004(2004), No. 134, pp. 1-16.

Existence of infinitely many solutions for elliptic boundary-value problems with nonsymmetrical critical nonlinearity

Geng Di

Abstract:
In this paper, we study a semilinear elliptic boundary-value problem involving nonsymmetrical term with critical growth on a bounded smooth domain in 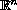$\mathbb{R}^n$. We show the existence of infinitely many weak solutions under the presence of some symmetric sublinear term, the corresponding critical values of the variational functional are negative and go to zero.

Submitted June 29, 2004. Published November 23, 2004.
Math Subject Classifications: 35B50, 35J40.
Key Words: Dirichlet problem; critical growth; non-symmetric perturbation; infinitely many solutions.

Show me the PDF file (255K), TEX file, and other files for this article.

Geng Di
Department of Mathematics
South China Normal University
Guangzhou, 510631, China
email: gengdi@scnu.edu.cn

Return to the EJDE web page