We prove the existence of solutions for the functional differential inclusion
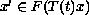 ,
where
,
where
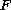 is
upper semi-continuous, compact-valued multifunction
such that
is
upper semi-continuous, compact-valued multifunction
such that
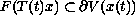 on
on
![$[0,T]$](gifs/ad.gif) ,
,
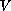 is a proper convex and lower semicontinuous function,
and
is a proper convex and lower semicontinuous function,
and
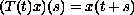 .
.
Vasile Lupulescu
Abstract:
We prove the existence of solutions for the functional
differential inclusion
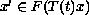 ,
where
,
where
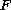 is
upper semi-continuous, compact-valued multifunction
such that
is
upper semi-continuous, compact-valued multifunction
such that
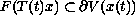 on
on
![$[0,T]$](gifs/ad.gif) ,
,
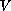 is a proper convex and lower semicontinuous function,
and
is a proper convex and lower semicontinuous function,
and
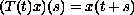 .
.
Submitted September 24, 2004. Published November 29, 2004.
Math Subject Classifications: 34A60, 34K05, 34K25.
Key Words: Functional differential inclusions; existence result.
Show me the PDF file (175K), TEX file for this article.
 |
Vasile Lupulescu Department of Mathematics "Constantin Brâncusi"- University of Târgu-Jiu Bulevardul Republicii, No. 1, 1400 Târgu-Jiu, Romania email: vasile@utgjiu.ro |
|---|
Return to the EJDE web page