Electron. J. Diff. Eqns., Vol. 2004(2004), No. 15, pp. 1-30.
The Heun equation and the Calogero-Moser-Sutherland system II:
Perturbation and algebraic solution
Kouichi Takemura
Abstract:
We apply a method of perturbation for the
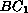 Inozemtsev model
from the trigonometric model and show the holomorphy of perturbation.
Consequently, the convergence of eigenvalues and eigenfuncions which
are expressed as formal power series is proved.
We investigate also the relationship between
Inozemtsev model
from the trigonometric model and show the holomorphy of perturbation.
Consequently, the convergence of eigenvalues and eigenfuncions which
are expressed as formal power series is proved.
We investigate also the relationship between
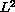 space and some
finite dimensional space of elliptic functions.
space and some
finite dimensional space of elliptic functions.
Submitted May 15, 2003. Published February 5, 2004.
Math Subject Classifications: 33E15, 81Q10.
Key Words: Heun equation, Calogero-Moser-Sutherland system,
Inozemtsev model, perturbation, Kato-Rellich theory,
trigonometric limit, Heun function, algebraic solution.
Show me the
PDF file (346K),
TEX file for this article.
 |
Kouichi Takemura
Department of Mathematical Sciences
Yokohama City University
22-2 Seto, Kanazawa-ku, Yokohama 236-0027, Japan
email: takemura@yokohama-cu.ac.jp |
|---|
Return to the EJDE web page
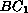 Inozemtsev model
from the trigonometric model and show the holomorphy of perturbation.
Consequently, the convergence of eigenvalues and eigenfuncions which
are expressed as formal power series is proved.
We investigate also the relationship between
Inozemtsev model
from the trigonometric model and show the holomorphy of perturbation.
Consequently, the convergence of eigenvalues and eigenfuncions which
are expressed as formal power series is proved.
We investigate also the relationship between
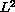 space and some
finite dimensional space of elliptic functions.
space and some
finite dimensional space of elliptic functions.
