Electron. J. Diff. Eqns., Vol. 2004(2004), No. 46, pp. 1-12.
An application of the dual variational principle
to a Hamiltonian system with discontinuous nonlinearities
Claudianor O. Alves, Daniel C. de Morais Filho,
& Marco Aurelio S. Souto
Abstract:
In this article, we study the existence of solutions to the
Hamiltonian elliptic system with discontinuous nonlinearities
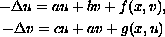
on a bounded subset of
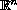 ,
with zero Dirichlet boundary
conditions. The functions
,
with zero Dirichlet boundary
conditions. The functions
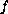 and
and
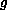 have a finite number of
jumping discontinuities.
have a finite number of
jumping discontinuities.
Submitted January 26, 2004. Published March 31, 2004.
Math Subject Classifications: 35J50, 37K05, 34A34.
Key Words: Hamiltonian systems, discontinuous nonlinearities,
dual variational principle.
Show me the
PDF file (250K),
TEX file for this article.
 |
Claudianor O. Alves
Departamento de Matematica e Estatistica
Universidade Federal de Campina Grande
Cx Postal 10044
58109-970-Campina Grande (PB), Brazil
email: coalves@dme.ufpb.br |
|---|
 |
Daniel C. de Morais Filho
Departamento de Matematica e Estatistica
Universidade Federal de Campina Grande
Cx Postal 10044
58109-970-Campina Grande (PB), Brazil
email: daniel@dme.ufpb.br |
|---|
 |
Marco Aurelio S. Souto
Departamento de Matematica e Estat}stica
Universidade Federal de Campina Grande
Cx Postal 10044
58109-970-Campina Grande (PB), Brazil
email: marco@dme.ufpb.br |
|---|
Return to the EJDE web page
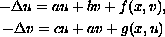
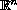 ,
with zero Dirichlet boundary
conditions. The functions
,
with zero Dirichlet boundary
conditions. The functions
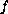 and
and
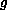 have a finite number of
jumping discontinuities.
have a finite number of
jumping discontinuities.


