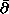 -equations on strongly
pseudo-convex domains with
-equations on strongly
pseudo-convex domains with
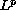 -estimates
-estimates
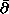 -equations on strongly
pseudo-convex domains with
-equations on strongly
pseudo-convex domains with
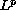 -estimates
-estimates
Osama Abdelkader & Shaban Khidr
Abstract:
We construct a solution to the
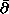 -equation on
a strongly pseudo-convex domain of a complex manifold.
This is done for forms of type
-equation on
a strongly pseudo-convex domain of a complex manifold.
This is done for forms of type
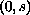 ,
,
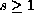 ,
with values in a holomorphic vector bundle which is Nakano
positive and for complex valued forms of type
,
with values in a holomorphic vector bundle which is Nakano
positive and for complex valued forms of type
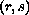 ,
,
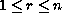 ,
when the complex manifold is a Stein manifold.
Using Kerzman's techniques, we find the
,
when the complex manifold is a Stein manifold.
Using Kerzman's techniques, we find the
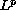 -estimates,
-estimates,
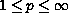 ,
for the solution.
,
for the solution.
Submitted March 01, 2004. Published May 20, 2004.
Math Subject Classifications: 32F27, 32C35, 35N15.
Key Words: L^p-estimates,
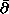 -equation,
strongly pseudo-convex, smooth boundary, complex manifolds.
-equation,
strongly pseudo-convex, smooth boundary, complex manifolds.
Show me the PDF file (243K), TEX file for this article.
 |
Osama Abdelkader Mathematics Department, Faculty of Science Minia University, El-Minia, Egypt email: usamakader882000@yahoo.com |
|---|---|
 |
Shaban Khidr Mathematics Department, Faculty of Science Cairo University, Beni- Suef, Egypt email: skhidr@yahoo.com |
Return to the EJDE web page