Electron. J. Diff. Eqns., Vol. 2005(2005), No. 103, pp. 1-8.
Periodic trajectories for evolution equations in Banach spaces
Mircea D. Voisei
Abstract:
The existence of periodic solutions for the evolution
equation
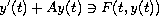
is investigated under considerably simple assumptions on
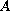 and
and
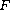 .
Here
.
Here
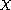 is a Banach space, the operator
is a Banach space, the operator
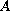 is
is
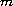 -accretive,
-accretive,
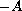 generates a compact semigroup,
and
generates a compact semigroup,
and
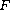 is a Caratheodory mapping. Two examples
concerning nonlinear parabolic equations are presented.
is a Caratheodory mapping. Two examples
concerning nonlinear parabolic equations are presented.
Submitted August 3, 2005. Published September 28, 2005.
Math Subject Classifications: 47J35, 34C25, 35K55.
Key Words: Periodic solution, evolution equation of parabolic type.
Show me the
PDF file (222K),
TEX file for this article.
 |
Mircea D. Voisei
Department of Mathematics
MAGC 3.734, The University of Texas - Pan American
Edinburg, TX 78539, USA
email: mvoisei@utpa.edu |
|---|
Return to the EJDE web page
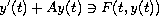
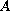 and
and
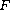 .
Here
.
Here
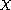 is a Banach space, the operator
is a Banach space, the operator
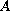 is
is
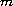 -accretive,
-accretive,
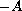 generates a compact semigroup,
and
generates a compact semigroup,
and
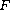 is a Caratheodory mapping. Two examples
concerning nonlinear parabolic equations are presented.
is a Caratheodory mapping. Two examples
concerning nonlinear parabolic equations are presented.
