We study the vanishing of solutions of the Cauchy problem for the equation
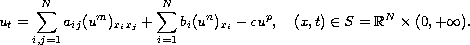
Obtained results depend on relations of parameters of the problem and growth of initial data at infinity.
Alexander Gladkov, Sergey Prokhozhy
Abstract:
We study the vanishing of solutions of the Cauchy problem for
the equation
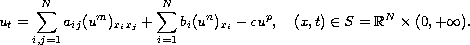
Obtained results depend on relations of parameters
of the problem and growth of initial data at infinity.
Submitted June 10, 2005. Published October 17, 2005.
Math Subject Classifications: 35K55, 35K65.
Key Words: Diffusion equation; vanishing of solutions.
Show me the PDF file (314K), TEX file for this article.
 |
Alexander Gladkov Mathematics Department, Vitebsk State University Moskovskii pr. 33, 210038 Vitebsk, Belarus email: gladkov@vsu.by |
|---|---|
 |
Sergey Prokhozhy Mathematics Department, Vitebsk State University Moskovskii Pr. 33, 210038 Vitebsk, Belarus email: prokhozhy@vsu.by |
Return to the EJDE web page