Dragos-Patru Covei
Abstract:
We prove the existence of a unique positive solution to the problem
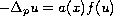
in
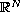 ,
,
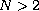 .
Our result extended previous works by
Cirstea-Radulescu and Dinu, while the proofs are based on two
theorems on bounded domains, due to Diaz-Saa and Goncalves-Santos.
.
Our result extended previous works by
Cirstea-Radulescu and Dinu, while the proofs are based on two
theorems on bounded domains, due to Diaz-Saa and Goncalves-Santos.
Submitted June 8, 2005. Published December 5, 2005.
Math Subject Classifications: 35J60, 35J70.
Key Words: Quasilinear elliptic problem; uniqueness; existence;
nonexistence; lower-upper solutions.
A corrigendum was posted on October 8, 2007. Some misprints are corrected and the existence of solutions is clarified. Please see the last page of this manuscript.
Show me the PDF file (245K), TEX file for this article.
 |
Dragos-Patru Covei Constantin Brancusi' University of Targu-Jiu Bulevardul Republicii, nr. 1 210152 Targu-Jiu, Romania email: dragoscovei77@yahoo.com |
|---|
Return to the EJDE web page