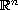
Faten Toumi, Noureddine Zeddini
Abstract:
Let
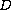 be an unbounded domain in
be an unbounded domain in
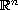 (
(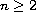 )
with a nonempty compact boundary
)
with a nonempty compact boundary
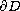 .
We consider the
following nonlinear elliptic problem, in the sense of distributions,
.
We consider the
following nonlinear elliptic problem, in the sense of distributions,
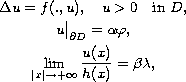
where
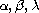 are nonnegative constants with
are nonnegative constants with
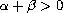 and
and
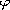 is a nontrivial nonnegative
continuous function on
is a nontrivial nonnegative
continuous function on
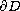 .
The function
.
The function
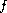 is nonnegative and satisfies some appropriate conditions related
to a Kato class of functions, and
is nonnegative and satisfies some appropriate conditions related
to a Kato class of functions, and
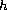 is a fixed harmonic
function in
is a fixed harmonic
function in
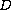 , continuous on
, continuous on
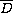 .
Our aim is to prove
the existence of positive continuous solutions bounded below by a
harmonic function. For this aim we use the Schauder fixed-point
argument and a potential theory approach.
.
Our aim is to prove
the existence of positive continuous solutions bounded below by a
harmonic function. For this aim we use the Schauder fixed-point
argument and a potential theory approach.
Submitted September 30, 2005. Published December 8, 2005.
Math Subject Classifications: 34B15, 34B27.
Key Words: Green function; nonlinear elliptic equation;
positive solution; Schauder fixed point theorem.
Show me the PDF file (286K), TEX file for this article.
 |
Faten Toumi Département de Mathématiques Faculté des Sciences de Tunis Campus Universitaire, 2092 Tunis, Tunisia email: Faten.Toumi@fsb.rnu.tn |
|---|---|
 |
Noureddine Zeddini Département de Mathématiques Faculté des Sciences de Tunis Campus Universitaire, 2092 Tunis, Tunisia email: Noureddine.Zeddini@ipein.rnu.tn |
Return to the EJDE web page