Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 145, pp. 1-9.
Zeros of the Jost function for a class of exponentially
decaying potentials
Daphne Gilbert, Alain Kerouanton
Abstract:
We investigate the properties of a series representing the Jost
solution for the differential equation
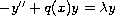 ,
,
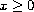 ,
,
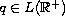 .
Sufficient conditions are determined on the real or complex-valued
potential
.
Sufficient conditions are determined on the real or complex-valued
potential
 for the series to converge and bounds are obtained
for the sets of eigenvalues, resonances and spectral singularities
associated with a corresponding class of Sturm-Liouville operators.
In this paper, we restrict our investigations to the class of
potentials
for the series to converge and bounds are obtained
for the sets of eigenvalues, resonances and spectral singularities
associated with a corresponding class of Sturm-Liouville operators.
In this paper, we restrict our investigations to the class of
potentials
 satisfying
satisfying
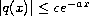 ,
,
 ,
for some
,
for some
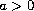 and
and
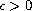 .
.
Submitted October 4, 2005. Published December 8, 2005.
Math Subject Classifications: 34L40, 35B34, 35P15, 33C10.
Key Words: Jost solution; Sturm-Liouville operators;
resonances; eigenvalues; spectral singularities.
Show me the
PDF file (211K),
TEX file for this article.
 |
Daphne Gilbert
School of Mathematical Sciences
Dublin Institute of Technology
Kevin Street, Dublin 8, Ireland
email: daphne.gilbert@dit.ie |
|---|
 |
Alain Kerouanton
School of Mathematical Sciences
Dublin Institute of Technology
Kevin Street, Dublin 8, Ireland
email: alainkerouanton@hotmail.com Fax: +35314024994 |
|---|
Return to the EJDE web page
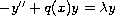 ,
,
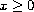 ,
,
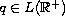 .
Sufficient conditions are determined on the real or complex-valued
potential
.
Sufficient conditions are determined on the real or complex-valued
potential
 for the series to converge and bounds are obtained
for the sets of eigenvalues, resonances and spectral singularities
associated with a corresponding class of Sturm-Liouville operators.
In this paper, we restrict our investigations to the class of
potentials
for the series to converge and bounds are obtained
for the sets of eigenvalues, resonances and spectral singularities
associated with a corresponding class of Sturm-Liouville operators.
In this paper, we restrict our investigations to the class of
potentials
 satisfying
satisfying
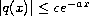 ,
,
 ,
for some
,
for some
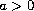 and
and
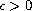 .
.

