Electron. J. Diff. Eqns., Vol. 2005(2005), No. 16, pp. 1-8.
Estimates for solutions to nonlinear boundary-value
problems in conic domains
Tahir S. Gadjiev, Sardar Y. Aliev
Abstract:
We obtain sharp estimates on the solution and its
derivative near the conic points. In particular,
we show that the solution satisfies
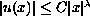 where lambda is an eigenvalue of the Sturm-Liouville problem.
Also we prove that the solution has square summable
weighted second generalized derivatives.
where lambda is an eigenvalue of the Sturm-Liouville problem.
Also we prove that the solution has square summable
weighted second generalized derivatives.
An addendum has been attached on March 18, 2005.
It includes the reference
Borsuk, M. V.;
Behavior of generalized solutions of the Dirichlet problem for
second-order quasilinear elliptic equations of divergence type near a
conical point. (Russian)
Sibirsk. Mat. Zh. 31 (1990), no. 6, 25--38; translation in Siberian
Math. J. 31 (1990), no. 6, 891--904 (1991)
and compares the results in this article with those in the new reference.
Submitted January 27, 2004. Published February 1, 2005.
Math Subject Classifications: 35J20, 35D10.
Key Words: Nonlinear equation; behavior of solutions; nonsmooth domain.
Show me the
PDF file (223K),
TEX file for this article.
 |
Tahir S. Gadjiev
Institute of Mathematics & Mechanics of NAS Azerbaijan
Department of Nonlinear Analysis
9, F. Agayev str., AZ1141, Baku, Azerbaijan
email: tgadjiev@mail.az |
|---|
 |
Sardar Y. Aliev
Baku State University, Department of Mathematics
23 Z. Khalilov str., AZ1148, Baku, Azerbaijan
email: ibvag@yahoo.com |
|---|
Return to the EJDE web page
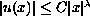 where lambda is an eigenvalue of the Sturm-Liouville problem.
Also we prove that the solution has square summable
weighted second generalized derivatives.
where lambda is an eigenvalue of the Sturm-Liouville problem.
Also we prove that the solution has square summable
weighted second generalized derivatives. 
