Electron. J. Diff. Eqns., Vol. 2005(2005), No. 21, pp. 1-7.
Continuous selections of set of mild solutions of evolution inclusions
Annamalai Anguraj, Chinnagounder Murugesan
Abstract:
We prove the existence of continuous selections of the set
valued map
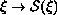 where
where
 is the set of all mild solutions of the
evolution inclusions of the form
is the set of all mild solutions of the
evolution inclusions of the form
![$$\displaylines{
\dot{x}(t) \in A(t)x(t)+\int_0^tK(t,s)F(s,x(s))ds \cr
x(0)=\xi ,\quad t\in I=[0,T],
}$$](gifs/ac.gif)
where
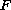 is a lower semi continuous set valued map Lipchitzean
with respect to
is a lower semi continuous set valued map Lipchitzean
with respect to
 in a separable Banach space
in a separable Banach space
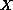 ,
,
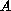 is the infinitesimal generator of a
is the infinitesimal generator of a
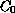 -semi group of
bounded linear operators from
-semi group of
bounded linear operators from
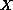 to
to
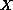 ,
and
,
and
 is a
continuous real valued function defined on
is a
continuous real valued function defined on
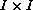 with
with
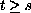 for all
for all
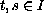 and
and
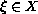 .
.
Submitted November 3, 2004. Published February 11, 2005.
Math Subject Classifications: 34A60, 34G20.
Key Words: Mild solutions; differential inclusions;
integrodifferential inclusions.
Show me the
PDF file (193K),
TEX file for this article.
 |
Annamalai Anguraj
Department of Mathematics
P.S.G. College of Arts & Science
Coimbatore - 641 014, Tamilnadu, India
email: angurajpsg@yahoo.com
|
|---|
 |
Chinnagounder Murugesan
Department of Mathematics
Gobi Arts & Science College
Gobichettipalayam - 638 453, Tamilnadu, India
|
|---|
Return to the EJDE web page
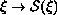 where
where
 is the set of all mild solutions of the
evolution inclusions of the form
is the set of all mild solutions of the
evolution inclusions of the form
![$$\displaylines{
\dot{x}(t) \in A(t)x(t)+\int_0^tK(t,s)F(s,x(s))ds \cr
x(0)=\xi ,\quad t\in I=[0,T],
}$$](gifs/ac.gif)
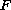 is a lower semi continuous set valued map Lipchitzean
with respect to
is a lower semi continuous set valued map Lipchitzean
with respect to
 in a separable Banach space
in a separable Banach space
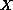 ,
,
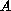 is the infinitesimal generator of a
is the infinitesimal generator of a
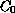 -semi group of
bounded linear operators from
-semi group of
bounded linear operators from
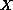 to
to
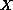 ,
and
,
and
 is a
continuous real valued function defined on
is a
continuous real valued function defined on
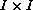 with
with
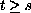 for all
for all
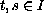 and
and
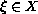 .
.

