Electron. J. Diff. Eqns., Vol. 2005(2005), No. 36, pp. 1-20.
An Lp-approach for the study of degenerate
parabolic equations
Rabah Labbas, Ahmed Medeghri, Boubaker-Khaled Sadallah
Abstract:
We give regularity results for solutions of a parabolic equation
in non-rectangular domains
![$U=\cup_{t\in ] 0,1[}\{ t\} \times I_{t}$](gifs/aa.gif) with
with
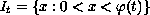 .
The optimal regularity is obtained in the framework of the space
.
The optimal regularity is obtained in the framework of the space
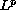 with
with
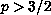 by considering the following cases:
(1) When
by considering the following cases:
(1) When
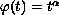 ,
,
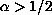 with a regular right-hand side belonging to a subspace
of
with a regular right-hand side belonging to a subspace
of
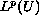 and under assumption
and under assumption
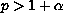 .
We use Labbas-Terreni results [11].
(2) When
.
We use Labbas-Terreni results [11].
(2) When
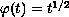 with a right-hand side taken only
in
with a right-hand side taken only
in
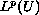 .
Our approach make use of the celebrated Dore-Venni
results [2].
.
Our approach make use of the celebrated Dore-Venni
results [2].
Submitted July 16, 2004. Published March 29, 2005.
Math Subject Classifications: 35K05, 35K65, 35K90
Key Words: Sum of linear operators, diffusion equation,
non rectangular domain,bounded imaginary powers of operators
Show me the
PDF file (296K),
TEX file for this article.
 |
Rabah Labbas
Laboratoire de Mathématiques
Université du Havre, U.F.R. Sciences et Techniques
b.p. 540, 76058 Le Havre, France
email: labbas@univ-lehavre.fr |
|---|
| |
Ahmed Medeghri
Université de Mostaganem
b.p. 188, 27000, Mostaganem, Algeria
email: medeghri@univ-mosta.dz |
|---|
| |
Boubaker-Khaled Sadallah
Ecole Normale Supérieure, Département
de Maths, 16050 Kouba, Alger, Algeria
email: sadallah@wissal.dz |
|---|
Return to the EJDE web page
![$U=\cup_{t\in ] 0,1[}\{ t\} \times I_{t}$](gifs/aa.gif) with
with
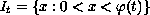 .
The optimal regularity is obtained in the framework of the space
.
The optimal regularity is obtained in the framework of the space
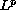 with
with
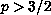 by considering the following cases:
(1) When
by considering the following cases:
(1) When
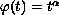 ,
,
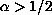 with a regular right-hand side belonging to a subspace
of
with a regular right-hand side belonging to a subspace
of
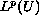 and under assumption
and under assumption
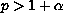 .
We use Labbas-Terreni results [11].
(2) When
.
We use Labbas-Terreni results [11].
(2) When
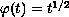 with a right-hand side taken only
in
with a right-hand side taken only
in
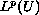 .
Our approach make use of the celebrated Dore-Venni
results [2].
.
Our approach make use of the celebrated Dore-Venni
results [2].
