Electron. J. Diff. Eqns., Vol. 2005(2005), No. 54, pp. 1-22.
Local stability of spike steady states in a simplified
Gierer-Meinhardt system
Georgi E. Karadzhov, David Edmunds, Pieter de Groen
Abstract:
In this paper we study the stability of the single internal spike
solution of a simplified Gierer-Meinhardt' system of equations
in one space dimension.
The linearization around this spike consists of a selfadjoint
differential operator plus a non-local term, which is a non-selfadjoint
compact integral operator.
We find the asymptotic behaviour of the small eigenvalues and we prove
stability of the steady state for the parameter
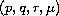 in a
four-dimensional region (the same as for the shadow equation,
[8]) and for any finite
in a
four-dimensional region (the same as for the shadow equation,
[8]) and for any finite
 if
if
 is sufficiently small.
Moreover, there exists an exponentially large
is sufficiently small.
Moreover, there exists an exponentially large
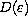 such that
the stability is still valid for
such that
the stability is still valid for
 . Thus we extend the
previous results known only for the case
. Thus we extend the
previous results known only for the case
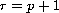 or
or
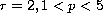 .
.
Submitted March 3, 2005. Published May 23, 2005.
Math Subject Classifications: 35B25, 35K60.
Key Words: Spike solution; singular perturbations;
reaction-diffusion equations; Gierer-Meinhardt equations.
Show me the
PDF file (319K),
TEX file for this article.
 |
Georgi E. Karadzhov
Institute for Mathematics and Informatics
Bulgarian academy of Sciences
1113 Sofia, Bulgaria
email: geremika@math.bas.bg |
|---|
 |
David E. Edmunds
Department of Mathematics
University of Sussex
Brighton BN1 9RF, U. K.
email: d.e.edmunds@sussex.ac.uk |
|---|
 |
Pieter P. N. de Groen
Department of Mathematics
Vrije Universiteit Brussel
Pleinlaan 2, B-1050 Brussels, Belgium
email: pdegroen@vub.ac.be |
|---|
Return to the EJDE web page
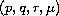 in a
four-dimensional region (the same as for the shadow equation,
[8]) and for any finite
in a
four-dimensional region (the same as for the shadow equation,
[8]) and for any finite
 if
if
 is sufficiently small.
Moreover, there exists an exponentially large
is sufficiently small.
Moreover, there exists an exponentially large
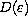 such that
the stability is still valid for
such that
the stability is still valid for
 . Thus we extend the
previous results known only for the case
. Thus we extend the
previous results known only for the case
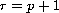 or
or
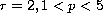 .
.


