Let
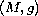 be a complete Riemannian manifold with metric
be a complete Riemannian manifold with metric
 and the Riemannian volume form
and the Riemannian volume form
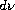 .
We consider the
.
We consider the
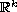 -valued
functions
-valued
functions
![$T\in [W^{-1,2}(M)\cap L_{loc}^{1}(M)]^{k}$](gifs/ae.gif) and
and
![$u\in [W^{1,2}(M)]^{k}$](gifs/af.gif) on
on
 ,
where
,
where
![$[W^{1,2}(M)]^{k}$](gifs/ah.gif) is a Sobolev space on
is a Sobolev space on
 and
and
![$[W^{-1,2}(M)]^{k}$](gifs/aj.gif) is its dual. We give a sufficient condition for the equality of
is its dual. We give a sufficient condition for the equality of
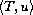 and the integral of
and the integral of
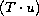 over
over
 ,
where
,
where
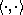 is the duality between
is the duality between
![$[W^{-1,2}(M)]^{k}$](gifs/aj.gif) and
and
![$[W^{1,2}(M)]^{k}$](gifs/ah.gif) .
This is an extension to
complete Riemannian manifolds of a result of H. Brezis and
F. E. Browder.
.
This is an extension to
complete Riemannian manifolds of a result of H. Brezis and
F. E. Browder.
