Electron. J. Diff. Eqns., Vol. 2005(2005), No. 79, pp. 1-25.
Solutions approaching polynomials at infinity to nonlinear
ordinary differential equations
Christos G. Philos, Panagiotis Ch. Tsamatos
Abstract:
This paper concerns the solutions approaching polynomials at
 to
to
 -th
order
(
-th
order
(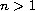 )
nonlinear ordinary differential
equations, in which the nonlinear term depends on time
)
nonlinear ordinary differential
equations, in which the nonlinear term depends on time
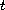 and on
and on
 , where
, where
 is the unknown function and
is the unknown function and
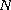 is an integer with
is an integer with
 .
For each given integer
.
For each given integer
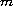 with
with
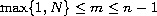 ,
conditions are given which
guarantee that, for any real polynomial of degree at most
,
conditions are given which
guarantee that, for any real polynomial of degree at most
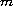 ,
there exists a solution that is asymptotic at
,
there exists a solution that is asymptotic at
 to this
polynomial. Sufficient conditions are also presented for every
solution to be asymptotic at
to this
polynomial. Sufficient conditions are also presented for every
solution to be asymptotic at
 to a real polynomial of
degree at most
to a real polynomial of
degree at most
 .
The results obtained extend those by the
authors and by Purnaras [25] concerning the particular case
.
The results obtained extend those by the
authors and by Purnaras [25] concerning the particular case
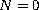 .
.
Submitted February 13, 2005. Published July 11, 2005.
Math Subject Classifications: 34E05, 34E10, 34D05
Key Words: Nonlinear differential equation; asymptotic properties;
asymptotic expansions; asymptotic to polynomials solutions.
Show me the
PDF file (337K),
TEX file for this article.
 |
Christos G. Philos
Department of Mathematics
University of Ioannina
P. O. Box 1186, 451 10 Ioannina, Greece
email: cphilos@cc.uoi.gr |
|---|
 |
P. Ch. Tsamatos
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: ptsamato@cc.uoi.gr |
|---|
Return to the EJDE web page
 to
to
 -th
order
(
-th
order
(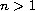 )
nonlinear ordinary differential
equations, in which the nonlinear term depends on time
)
nonlinear ordinary differential
equations, in which the nonlinear term depends on time
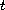 and on
and on
 , where
, where
 is the unknown function and
is the unknown function and
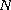 is an integer with
is an integer with
 .
For each given integer
.
For each given integer
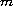 with
with
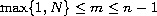 ,
conditions are given which
guarantee that, for any real polynomial of degree at most
,
conditions are given which
guarantee that, for any real polynomial of degree at most
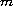 ,
there exists a solution that is asymptotic at
,
there exists a solution that is asymptotic at
 to this
polynomial. Sufficient conditions are also presented for every
solution to be asymptotic at
to this
polynomial. Sufficient conditions are also presented for every
solution to be asymptotic at
 to a real polynomial of
degree at most
to a real polynomial of
degree at most
 .
The results obtained extend those by the
authors and by Purnaras [25] concerning the particular case
.
The results obtained extend those by the
authors and by Purnaras [25] concerning the particular case
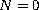 .
.

