Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 83, pp. 1-16.
Bifurcation diagram of a cubic three-parameter
autonomous system
Lenka Barakova, Evgenii P. Volokitin
Abstract:
In this paper, we study the cubic three-parameter autonomous planar system
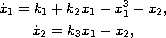
where
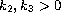 . Our goal is to obtain a
bifurcation diagram; i.e., to divide the parameter space into
regions within which the system has topologically equivalent phase
portraits and to describe how these portraits are transformed at
the bifurcation boundaries. Results may be applied to the
macroeconomical model IS-LM with Kaldor's assumptions. In this
model existence of a stable limit cycles has already been studied
(Andronov-Hopf bifurcation). We present the whole bifurcation
diagram and among others, we prove existence of more difficult
bifurcations and existence of unstable cycles.
. Our goal is to obtain a
bifurcation diagram; i.e., to divide the parameter space into
regions within which the system has topologically equivalent phase
portraits and to describe how these portraits are transformed at
the bifurcation boundaries. Results may be applied to the
macroeconomical model IS-LM with Kaldor's assumptions. In this
model existence of a stable limit cycles has already been studied
(Andronov-Hopf bifurcation). We present the whole bifurcation
diagram and among others, we prove existence of more difficult
bifurcations and existence of unstable cycles.
Submitted February 9, 2005. Published July 19, 2005.
Math Subject Classifications: 34C05, 34D45, 34C23.
Key Words: Phase portrait; bifurcation; central manifold;
topological equivalence; structural stability;
bifurcation diagram;limit cycle.
Show me the
PDF file (1366K),
TEX file for this article.
 |
Lenka Baráková
Mendel University, Dept. of Math.
Zemedelska 1, 613 00 Brno, Czech Rep.
email: barakova@mendelu.cz |
|---|
 |
Evgenii P. Volokitin
Sobolev Institute of Mathematics
Novosibirsk, 630090, Russia
email: volok@math.nsc.ru |
|---|
Return to the EJDE web page
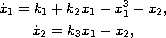
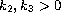 . Our goal is to obtain a
bifurcation diagram; i.e., to divide the parameter space into
regions within which the system has topologically equivalent phase
portraits and to describe how these portraits are transformed at
the bifurcation boundaries. Results may be applied to the
macroeconomical model IS-LM with Kaldor's assumptions. In this
model existence of a stable limit cycles has already been studied
(Andronov-Hopf bifurcation). We present the whole bifurcation
diagram and among others, we prove existence of more difficult
bifurcations and existence of unstable cycles.
. Our goal is to obtain a
bifurcation diagram; i.e., to divide the parameter space into
regions within which the system has topologically equivalent phase
portraits and to describe how these portraits are transformed at
the bifurcation boundaries. Results may be applied to the
macroeconomical model IS-LM with Kaldor's assumptions. In this
model existence of a stable limit cycles has already been studied
(Andronov-Hopf bifurcation). We present the whole bifurcation
diagram and among others, we prove existence of more difficult
bifurcations and existence of unstable cycles.

