

Hassan M. Serag, Eada A. El-Zahrani
Abstract:
In this paper, we study the following non-linear system on
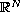
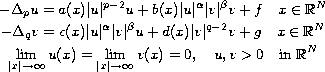
where
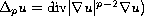 with
with
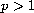 and
and
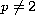 is the ``p-Laplacian",
is the ``p-Laplacian",
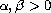 ,
,
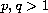 ,
and
,
and
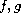 are given functions.
We obtain necessary and sufficient conditions for having a
maximum principle; then we use an approximation method to prove the
existence of positive solution for this system.
are given functions.
We obtain necessary and sufficient conditions for having a
maximum principle; then we use an approximation method to prove the
existence of positive solution for this system.
Submitted May 19, 2005. Published July 27, 2005.
Math Subject Classifications:
Key Words: aximum principle; nonlinear elliptic systems;
 -Laplacian;
sub and super solutions.
-Laplacian;
sub and super solutions.
Show me the PDF file (254K), TEX file for this article.
 |
Hassan M. Serag Mathematics Department, Faculty of Science Al-Azhar University Nasr City (11884), Cairo, Egypt email: serraghm@yahoo.com |
|---|---|
| Eada A. El-Zahrani Mathematics Department, Faculty of Science for Girls Dammam, P. O. Box 838, Pincode 31113, Saudi Arabia email: eada00@hotmail.com |
Return to the EJDE web page