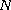 -point vortex system with random
intensities on
-point vortex system with random
intensities on

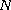 -point vortex system with random
intensities on
-point vortex system with random
intensities on

Cassio Neri
Abstract:
The system of
N
-point vortices on
 is considered
under the hypothesis that vortex intensities are independent and
identically distributed random variables with respect to a law
is considered
under the hypothesis that vortex intensities are independent and
identically distributed random variables with respect to a law
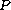 supported on
supported on
![$(0,1]$](gifs/ad.gif) . It is shown that, in the limit as
. It is shown that, in the limit as
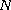 approaches
approaches
 ,
the 1-vortex distribution is a minimizer of
the free energy functional and is associated to (some) solutions
of the following non-linear Poisson Equation:
,
the 1-vortex distribution is a minimizer of
the free energy functional and is associated to (some) solutions
of the following non-linear Poisson Equation:
![$$
-\Delta u(x) = C^{-1}\int_{(0,1]} r\hbox{e}^{-\beta ru(x)-
\gamma r|x|^2}P(\hbox{d}r), \quad\forall x\in \mathbb{R}^2,
$$](gifs/af.gif)
where
![$\displaystyle C = \int_{(0,1]}\int_{\mathbb{R}^2}\hbox{e}^{-\beta ru(y)
- \gamma r|y|^2}\hbox{d} yP(\hbox{d}r)$](gifs/ag.gif) .
.
Submitted March 3, 2005. Published August 24, 2005.
Math Subject Classifications: 76F55, 82B5.
Key Words: Statistical mechanics; N-point vortex system; Onsager theory;
mean field equation.
Show me the PDF file (328K), TEX file for this article.
 |
Cassio Neri Instituto de Matemática Universidade Federal do Rio de Janeiro Caixa Postal 68530, CEP: 21945-970, Rio de Janeiro, Brazil email: cassio@labma.ufrj.br |
|---|
Return to the EJDE web page