Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 02, pp. 1-8.
Existence of large solutions for a semilinear elliptic
problem via explosive sub- supersolutions
Zhijun Zhang
Abstract:
We consider the boundary blow-up nonlinear elliptic problems
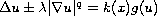 in a bounded
domain with boundary condition
in a bounded
domain with boundary condition
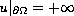 ,
where
,
where
![$q\in [0, 2]$](gifs/ac.gif) and
and
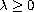 .
Under suitable growth assumptions on
.
Under suitable growth assumptions on
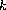 near the boundary
and on
near the boundary
and on
 both at zero and at infinity, we show the existence
of at least one solution in
both at zero and at infinity, we show the existence
of at least one solution in
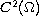 .
Our proof is based on the method of explosive sub-supersolutions,
which permits positive weights
.
Our proof is based on the method of explosive sub-supersolutions,
which permits positive weights
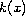 which are unbounded
and/or oscillatory near the boundary. Also, we show
the global optimal asymptotic behaviour of the solution
in some special cases.
which are unbounded
and/or oscillatory near the boundary. Also, we show
the global optimal asymptotic behaviour of the solution
in some special cases.
Submitted May 21, 2005. Published January 6, 2006.
Math Subject Classifications: 35J60, 35B25, 35B50, 35R05.
Key Words: Semilinear elliptic equations; explosive subsolutions;
explosive superbsolutions; existence;
global optimal asymptotic behaviour.
Show me the
PDF file (225K),
TEX file for this article.
 |
Zhijun Zhang
Department of Mathematics and Informational Science
Yantai University, Yantai, Shandong, 264005, China
email: zhangzj@ytu.edu.cn |
|---|
Return to the EJDE web page
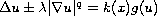 in a bounded
domain with boundary condition
in a bounded
domain with boundary condition
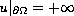 ,
where
,
where
![$q\in [0, 2]$](gifs/ac.gif) and
and
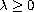 .
Under suitable growth assumptions on
.
Under suitable growth assumptions on
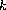 near the boundary
and on
near the boundary
and on
 both at zero and at infinity, we show the existence
of at least one solution in
both at zero and at infinity, we show the existence
of at least one solution in
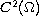 .
Our proof is based on the method of explosive sub-supersolutions,
which permits positive weights
.
Our proof is based on the method of explosive sub-supersolutions,
which permits positive weights
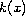 which are unbounded
and/or oscillatory near the boundary. Also, we show
the global optimal asymptotic behaviour of the solution
in some special cases.
which are unbounded
and/or oscillatory near the boundary. Also, we show
the global optimal asymptotic behaviour of the solution
in some special cases.
