Electron. J. Diff. Eqns., Vol. 2006(2006), No. 117, pp. 1-11.

Existence and uniqueness of periodic solutions for first-order neutral functional differential equations with two deviating arguments

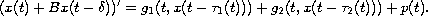
Jinsong Xiao, Bingwen Liu

Abstract:
In this paper, we use the coincidence degree theory to establish the existence and uniqueness of T-periodic solutions for the first-order neutral functional differential equation, with two deviating arguments,
$$ (x(t)+Bx(t-\delta))'= g_{1}(t,x(t-\tau_{1}(t)))+g_{2}(t,x(t-\tau_{2}(t))) +p(t). $$

Submitted March 16, 2006. Published September 26, 2006.
Math Subject Classifications: 34C25, 34D40.
Key Words: First order; neutral; functional differential equations; deviating argument; periodic solutions; coincidence degree.

Show me the PDF file (225K), TEX file for this article.

Jinsong Xiao
Department of Mathematics and Computer Science
Hunan City University
Yiyang, Hunan 413000, China
email: bingxiao209@yahoo.com.cn
Bingwen Liu
College of Mathematics and Information Science
Jiaxing University
Jiaxing, Zhejiang 314001, China
email: liubw007@yahoo.com.cn

Return to the EJDE web page