The endpoint Strichartz estimate
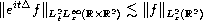
is known to be false by the work of Montgomery-Smith [2], despite being only "logarithmically far" from being true in some sense. In this short note we show that (in sharp contrast to the
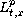 Strichartz estimates) the situation is not improved by passing
to a bilinear setting; more precisely, if
Strichartz estimates) the situation is not improved by passing
to a bilinear setting; more precisely, if
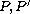 are non-trivial
smooth Fourier cutoff multipliers then we show that
the bilinear estimate
are non-trivial
smooth Fourier cutoff multipliers then we show that
the bilinear estimate

fails even when
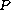 ,
,
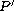 have widely separated supports.
have widely separated supports.
