Electron. J. Diff. Eqns., Vol. 2006(2006), No. 16, pp. 1-19.
Inverse spectral analysis for singular
differential operators with matrix coefficients
Nour el Houda Mahmoud, Imen Yaich
Abstract:
Let
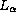 be the Bessel operator with
matrix coefficients defined on
be the Bessel operator with
matrix coefficients defined on
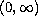 by
by
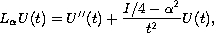
where
 is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
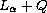 kind and its
various properties from only its spectral characteristics.
Here
kind and its
various properties from only its spectral characteristics.
Here
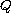 is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.
is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.
Submitted October 14, 2005. Published February 2, 2006.
Math Subject Classifications: 45Q05, 45B05, 45F15, 34A55, 35P99.
Key Words: Inverse problem; Fourier-Bessel transform;
spectral measure; Hilbert-Schmidt operator;
Fredholm's equation.
Show me the
PDF file (105K),
TEX file for this article.
Nour el Houda Mahmoud
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 1060 Tunis, Tunisia
email: houda.mahmoud@fst.rnu.tn
|
Imen Yaïch
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 1060 Tunis, Tunisia
email: imen.maalej@fst.rnu.tn
|
Return to the EJDE web page
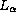 be the Bessel operator with
matrix coefficients defined on
be the Bessel operator with
matrix coefficients defined on
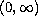 by
by
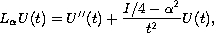
 is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
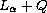 kind and its
various properties from only its spectral characteristics.
Here
kind and its
various properties from only its spectral characteristics.
Here
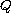 is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.
is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.