Electron. J. Diff. Eqns., Vol. 2006(2006), No. 45, pp. 1-9.
Blow-up of solutions for an integro-differential equation with
a nonlinear source
Shun-Tang Wu
Abstract:
We study the nonlinear viscoelastic wave equation
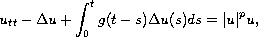
in a bounded domain, with the initial and Dirichlet boundary conditions.
By modifying the method in [15], we prove that there are solutions,
under some conditions on the initial data, which blow up in finite time
with nonpositive initial energy as well as positive initial energy.
Estimates of the lifespan of solutions are also given.
Submitted February 7, 2006. Published April 6, 2006.
Math Subject Classifications: 35L05, 35L15, 35L70, 37B25.
Key Words: Blow-up; life span; viscoelastic; integro-differential equation.
Show me the
PDF file (216K),
TEX file for this article.
 |
Shun-Tang Wu
General Educational Center
China University of Technology
Taipei, 116, Taiwan
email: stwu@cute.edu.tw |
|---|
Return to the EJDE web page