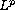Electron. J. Diff. Eqns., Vol. 2006(2006), No. 48, pp. 1-16.

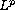$L^p$-resolvent estimates and time decay for generalized thermoelastic plate equations

Robert Denk, Reinhard Racke

Abstract:
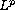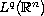We consider the Cauchy problem for a coupled system generalizing the thermoelastic plate equations. First we prove resolvent estimates for the stationary operator and conclude the analyticity of the associated semigroup in $L^p$-spaces, 1 less than p less than $\infty$, for certain values of the parameters of the system; here the Newton polygon method is used. Then we prove decay rates of the $L^q(\mathbb{R}^n)$-norms of solutions, 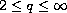$2\leq q\leq\infty$, as time tends to infinity.

Submitted September 13, 2005. Published April 11, 2006.
Math Subject Classifications: 35M20, 35B40, 35Q72, 47D06, 74F05.
Key Words: Analytic semigroup in 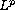$L^p$; polynomial decay rates; Cauchy problem.

Show me the PDF file (306K), TEX file, and other files for this article.

Robert Denk
Department of Mathematics and Statistics
University of Konstanz, 78457 Konstanz, Germany
email: robert.denk@uni-konstanz.de
Reinhard Racke
Department of Mathematics and Statistics
University of Konstanz, 78457 Konstanz, Germany
email: reinhard.racke@uni-konstanz.de

Return to the EJDE web page