Electron. J. Diff. Eqns., Vol. 2006(2006), No. 65, pp. 1-13.
Energy decay for solutions to semilinear systems of
elastic waves in exterior domains
Marcio V. Ferreira, Gustavo P. Menzala
Abstract:
We consider the dynamical system of elasticity in the exterior
of a bounded open domain in 3-D with smooth boundary.
We prove that under the effect of "weak" dissipation, the total
energy decays at a uniform rate as
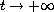 , provided the
initial data is "small" at infinity. No assumptions on the
geometry of the obstacle are required. The results are then
applied to a semilinear problem proving global existence and
decay for small initial data.
, provided the
initial data is "small" at infinity. No assumptions on the
geometry of the obstacle are required. The results are then
applied to a semilinear problem proving global existence and
decay for small initial data.
Submitted March 20, 2006. Published May 22, 2006.
Math Subject Classifications: 35Q99, 35L99.
Key Words: Uniform stabilization; exterior domain; system of elastic waves;
semilinear problem.
Show me the
PDF file (254K),
TEX file for this article.
 |
Marcio V. Ferreira
Centro Universitá:rio Franciscano,
Rua dos Andradas 1614
Santa Maria, CEP 97010-032, RS, Brazil
email: ferreira@unifra.br |
|---|
 |
Gustavo Perla Menzala
National Laboratory of Scientific Computation LNCC/MCT
Av. Getulio Vargas 333, Petropolis, CEP 25651-070, RJ, Brasil
and IM-UFRJ, P.O. Box 68530, RJ, Brazil
email: perla@lncc.br |
|---|
Return to the EJDE web page
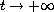 , provided the
initial data is "small" at infinity. No assumptions on the
geometry of the obstacle are required. The results are then
applied to a semilinear problem proving global existence and
decay for small initial data.
, provided the
initial data is "small" at infinity. No assumptions on the
geometry of the obstacle are required. The results are then
applied to a semilinear problem proving global existence and
decay for small initial data.

