Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 127, pp. 1-10.
Existence and localization of solutions
for fourth-order boundary-value problems
Ricardo Enguiça, Luis Sanchez
Abstract:
In this paper, we study the existence of solutions for the
differential equation
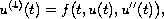
where
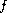 satisfies one-sided Lipschitz conditions with respect
to
satisfies one-sided Lipschitz conditions with respect
to
 and
and
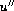 ,
with periodic conditions or boundary conditions
from "simply supported" beam theory.
We assume the existence of lower and upper solutions
(well-ordered and in some cases reversely ordered) and we make
use of a fourth-order linear differential operator factorization.
,
with periodic conditions or boundary conditions
from "simply supported" beam theory.
We assume the existence of lower and upper solutions
(well-ordered and in some cases reversely ordered) and we make
use of a fourth-order linear differential operator factorization.
Submitted July 20, 2007. Published September 28, 2007.
Math Subject Classifications: 34B15, 34C25.
Key Words: Beam equation; fourth order boundary value problem;
maximum principles; lower and upper solutions; reversed order.
Show me the
PDF file (217 KB),
TEX file for this article.
 |
Ricardo Enguiça
Area Científica de Matemática
Instituto Superior de Engenharia de Lisboa
Rua Conselheiro Emídio Navarro, 1 - 1950-062 Lisboa, Portugal
email: rroque@dec.isel.ipl.pt
|
|---|
 |
Luís Sanchez
Faculdade de Ciências da Universidade de Lisboa
Avenida Professor Gama Pinto 2, 1649-003 Lisboa, Portugal
email: sanchez@ptmat.fc.ul.pt
|
|---|
Return to the EJDE web page
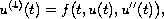
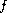 satisfies one-sided Lipschitz conditions with respect
to
satisfies one-sided Lipschitz conditions with respect
to
 and
and
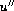 ,
with periodic conditions or boundary conditions
from "simply supported" beam theory.
We assume the existence of lower and upper solutions
(well-ordered and in some cases reversely ordered) and we make
use of a fourth-order linear differential operator factorization.
,
with periodic conditions or boundary conditions
from "simply supported" beam theory.
We assume the existence of lower and upper solutions
(well-ordered and in some cases reversely ordered) and we make
use of a fourth-order linear differential operator factorization.

