Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 147, pp. 1-30.
Multiscale elliptic-parabolic systems for flow and transport
Malgorzata Peszynska, Ralph E. Showalter
Abstract:
An upscaled elliptic-parabolic system of partial differential
equations describing the multiscale flow of a single-phase
incompressible fluid and transport of a dissolved chemical by
advection and diffusion through a heterogeneous porous medium is
developed without the usual assumptions of scale separation. After a
review of homogenization results for the traditional low contrast and
the
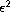 -scaled
high contrast cases, the new discrete upscaled
model based on local affine approximations is constructed. The
resulting model is mass conserving and contains the effects of local
advective transport as well as diffusion, it includes non-Fickian
models of dispersion and works over a broad range of contrast cases.
-scaled
high contrast cases, the new discrete upscaled
model based on local affine approximations is constructed. The
resulting model is mass conserving and contains the effects of local
advective transport as well as diffusion, it includes non-Fickian
models of dispersion and works over a broad range of contrast cases.
Submitted October 5, 2007. Published November 5, 2007.
Math Subject Classifications: 76S05, 35B27, 74Q15, 35R10.
Key Words: Upscaled porous media; double porosity models;
multiscale flow and transport; nonlocal dispersion
Show me the
PDF file (449 KB),
TEX file for this article.
 |
Malgorzata Peszynska
Department of Mathematics
Oregon State University, Corvallis, OR 97331, USA
email: mpesz@math.oregonstate.edu
|
|---|
 |
Ralph E. Showalter
Department of Mathematics
Oregon State University, Corvallis, OR 97331, USA
email: show@math.oregonstate.edu |
|---|
Return to the EJDE web page
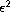 -scaled
high contrast cases, the new discrete upscaled
model based on local affine approximations is constructed. The
resulting model is mass conserving and contains the effects of local
advective transport as well as diffusion, it includes non-Fickian
models of dispersion and works over a broad range of contrast cases.
-scaled
high contrast cases, the new discrete upscaled
model based on local affine approximations is constructed. The
resulting model is mass conserving and contains the effects of local
advective transport as well as diffusion, it includes non-Fickian
models of dispersion and works over a broad range of contrast cases.

