Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 158, pp. 1-7.
Solution to nonlinear gradient dependent systems with a balance law
Zoubir Dahmani, Sebti Kerbal
Abstract:
In this paper, we are concerned with the initial boundary value
problem (IBVP) and with the Cauchy problem to the reaction-diffusion
system
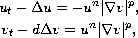
where
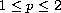 ,
d and n are positive real numbers.
Results on the existence and large-time behavior
of the solutions are presented.
,
d and n are positive real numbers.
Results on the existence and large-time behavior
of the solutions are presented.
Submitted April 15, 2007. Published November 21, 2007.
Math Subject Classifications: 35B40, 35B50, 35K57.
Key Words: Reaction-diffusion systems; global existence; asymptotic behavior;
maximum principle.
Show me the
PDF file (206 KB),
TEX file for this article.
 |
Zoubir Dahmani
Department of Mathematics, Faculty of Sciences
University of Mostaganem, Mostaganem, Algeria
email: zzdahmani@yahoo.fr |
|---|
 |
Sebti Kerbal
Department of Mathematics and Statistics
Sultan Qaboos Uiverstiy, Alkhod
Muscat, Sultanate of Oman
email: skerbal@squ.edu.om
|
|---|
Return to the EJDE web page
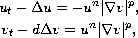
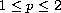 ,
d and n are positive real numbers.
Results on the existence and large-time behavior
of the solutions are presented.
,
d and n are positive real numbers.
Results on the existence and large-time behavior
of the solutions are presented.

