Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 175, pp. 1-10.
Self-adjoint boundary-value problems on time-scales
Fordyce A. Davidson, Bryan P. Rynne
Abstract:
In this paper we consider a second order, Sturm-Liouville-type
boundary-value operator of the form
![$$
L u := -[p u^{\nabla}]^{\Delta} + qu,
$$](gifs/aa.gif)
on an arbitrary, bounded time-scale
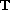 ,
for suitable
functions
,
for suitable
functions
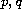 ,
together with suitable boundary conditions.
We show that, with a suitable choice of domain, this operator can
be formulated in the Hilbert space
,
together with suitable boundary conditions.
We show that, with a suitable choice of domain, this operator can
be formulated in the Hilbert space
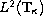 ,
in such a way that the resulting operator is self-adjoint,
with compact resolvent (here, "self-adjoint" means in the standard
functional analytic meaning of this term).
Previous discussions of operators of this, and similar, form have
described them as self-adjoint, but have not demonstrated
self-adjointness in the standard functional analytic sense.
,
in such a way that the resulting operator is self-adjoint,
with compact resolvent (here, "self-adjoint" means in the standard
functional analytic meaning of this term).
Previous discussions of operators of this, and similar, form have
described them as self-adjoint, but have not demonstrated
self-adjointness in the standard functional analytic sense.
Submitted June 6, 2007. Published December 12, 2007.
Math Subject Classifications: 34B05, 34L05, 39A05.
Key Words: Time-scales; boundary-value problem;
self-adjoint linear operators; Sobolev spaces.
Show me the
PDF file (230 KB),
TEX file for this article.
 |
Fordyce A. Davidson
Division of Mathematics, University of Dundee
Dundee, DD1 4HN, Scotland
email: fdavidso@maths.dundee.ac.uk |
|---|
 |
Bryan P. Rynne
Department of Mathematics and
the Maxwell Institute for Mathematical
Sciences
Heriot-Watt University, Edinburgh EH14 4AS,
Scotland
email: bryan@ma.hw.ac.uk |
|---|
Return to the EJDE web page
![$$
L u := -[p u^{\nabla}]^{\Delta} + qu,
$$](gifs/aa.gif)
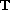 ,
for suitable
functions
,
for suitable
functions
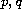 ,
together with suitable boundary conditions.
We show that, with a suitable choice of domain, this operator can
be formulated in the Hilbert space
,
together with suitable boundary conditions.
We show that, with a suitable choice of domain, this operator can
be formulated in the Hilbert space
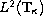 ,
in such a way that the resulting operator is self-adjoint,
with compact resolvent (here, "self-adjoint" means in the standard
functional analytic meaning of this term).
Previous discussions of operators of this, and similar, form have
described them as self-adjoint, but have not demonstrated
self-adjointness in the standard functional analytic sense.
,
in such a way that the resulting operator is self-adjoint,
with compact resolvent (here, "self-adjoint" means in the standard
functional analytic meaning of this term).
Previous discussions of operators of this, and similar, form have
described them as self-adjoint, but have not demonstrated
self-adjointness in the standard functional analytic sense.

