Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 20, pp. 1-10.
Positive solutions for a class of nonresonant
boundary-value problems
Xuemei Zhang
Abstract:
This paper concerns the existence and multiplicity of
positive solutions to the nonresonant second-order
boundary-value problem
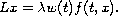
We are interested in the operator
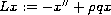 when
when
 is in
is in
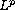 for
for
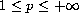 .
Our arguments are based on fixed point theorems in a cone
and Holder's inequality. The nonexistence of positive solutions
is also studied.
.
Our arguments are based on fixed point theorems in a cone
and Holder's inequality. The nonexistence of positive solutions
is also studied.
Submitted November 28, 2006. Published January 27, 2007.
Math Subject Classifications: 34B15.
Key Words: Positive solution; fixed point theorem;
existence; complete continuity.
Show me the
PDF file (208K),
TEX file for this article.
 |
Xuemei Zhang
Department of Mathematics and Physics
North China Electric Power University
Beijing 102206, China
email: zxm74@sina.com |
|---|
Return to the EJDE web page
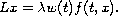
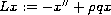 when
when
 is in
is in
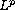 for
for
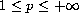 .
Our arguments are based on fixed point theorems in a cone
and Holder's inequality. The nonexistence of positive solutions
is also studied.
.
Our arguments are based on fixed point theorems in a cone
and Holder's inequality. The nonexistence of positive solutions
is also studied.
