Ginibre-Tsutsumi-Velo (1997) proved local well-posedness for the Zakharov system
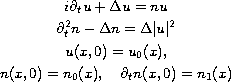
where
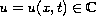 ,
,
 ,
,
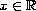 ,
and
,
and
 .
The proof was made
for any dimension
.
The proof was made
for any dimension
 , in the inhomogeneous Sobolev spaces
, in the inhomogeneous Sobolev spaces
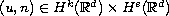 for a range
of exponents
for a range
of exponents
 ,
,
 depending on
depending on
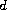 .
Here we restrict to dimension
.
Here we restrict to dimension
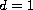 and present a few results establishing local ill-posedness
for exponent pairs
and present a few results establishing local ill-posedness
for exponent pairs
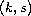 outside of the well-posedness regime.
The techniques employed are rooted in the work of Bourgain (1993),
Birnir-Kenig-Ponce-Svanstedt-Vega (1996), and Christ-Colliander-Tao (2003)
applied to the nonlinear Schrodinger equation.
outside of the well-posedness regime.
The techniques employed are rooted in the work of Bourgain (1993),
Birnir-Kenig-Ponce-Svanstedt-Vega (1996), and Christ-Colliander-Tao (2003)
applied to the nonlinear Schrodinger equation.