Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 45, pp. 1-10.
Positive solutions of a nonlinear higher order
boundary-value problem
John R. Graef, Johnny Henderson, Bo Yang
Abstract:
The authors consider the higher order boundary-value problem
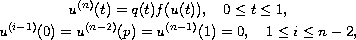
where
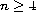 is an integer, and
is an integer, and
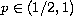 is a
constant. Sufficient conditions for the existence and nonexistence
of positive solutions of this problem are obtained. The main
results are illustrated with an example.
is a
constant. Sufficient conditions for the existence and nonexistence
of positive solutions of this problem are obtained. The main
results are illustrated with an example.
Submitted November 16, 2006. Published March 15, 2007.
Math Subject Classifications: 34B18.
Key Words: Existence and nonexistence of positive solutions;
Guo-Krasnosel'skii fixed point theorem;
higher order boundary value problem.
Show me the
PDF file (219K),
TEX file for this article.
 |
John R. Graef
Department of Mathematics
University of Tennessee at Chattanooga
Chattanooga, TN 37403, USA
email: John-Graef@utc.edu |
|---|
 |
Johnny Henderson
Department of Mathematics
Baylor University
Waco, TX 76798-7328, USA
email: Johnny_Henderson@baylor.edu |
|---|
 |
Bo Yang
Department of Mathematics
Kennesaw State University
Kennesaw, GA 30144, USA
email: byang@kennesaw.edu |
|---|
Return to the EJDE web page
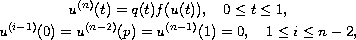
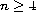 is an integer, and
is an integer, and
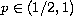 is a
constant. Sufficient conditions for the existence and nonexistence
of positive solutions of this problem are obtained. The main
results are illustrated with an example.
is a
constant. Sufficient conditions for the existence and nonexistence
of positive solutions of this problem are obtained. The main
results are illustrated with an example.


