We consider two natural problems arising in geometry which are equivalent to the local solvability of specific equations of Monge-Ampère type. These are: the problem of locally prescribed Gaussian curvature for surfaces in
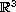 ,
and the local isometric embedding problem for two-dimensional
Riemannian manifolds. We prove a general local existence result
for a large class of degenerate Monge-Ampère equations in the
plane, and obtain as corollaries the existence of regular solutions
to both problems, in the case that the Gaussian curvature vanishes and
possesses a nonvanishing Hessian matrix at a critical point.
,
and the local isometric embedding problem for two-dimensional
Riemannian manifolds. We prove a general local existence result
for a large class of degenerate Monge-Ampère equations in the
plane, and obtain as corollaries the existence of regular solutions
to both problems, in the case that the Gaussian curvature vanishes and
possesses a nonvanishing Hessian matrix at a critical point.