The Navier-Stokes equations for the boundary layer are transformed, by a similarity transformation, into the ordinary Blasius differential equation which, together with appropriate boundary conditions constitutes the Blasius problem,
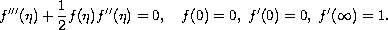
The well-posedness of the Navier-Stokes equations is an open problem. We solve this problem, in the case of constant flow in a boundary layer, by showing that the Blasius problem is ill-posed. If the second condition is replaced by
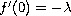 ,
then degeneracy occurs for
,
then degeneracy occurs for
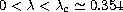 .
We investigate the problem
analytically to explain this phenomenon. We derive a simple equation
.
We investigate the problem
analytically to explain this phenomenon. We derive a simple equation
 ,
whose roots, for a fixed
,
whose roots, for a fixed
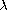 ,
determine the
solutions of the problem. It is found that the equation has exactly two
roots for
,
determine the
solutions of the problem. It is found that the equation has exactly two
roots for
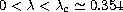 and no root beyond this point. Since
an arbitrarily small perturbation of the boundary condition gives rise to
an additional solution, which can be markedly different from the
unperturbed solution, the Blasius problem is ill-posed.
and no root beyond this point. Since
an arbitrarily small perturbation of the boundary condition gives rise to
an additional solution, which can be markedly different from the
unperturbed solution, the Blasius problem is ill-posed.