We prove the existence of nontrivial solutions for the singular critical problem
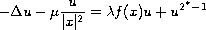
with Dirichlet boundary conditions. Here the domain is a smooth bounded subset of
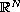 ,
,
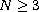 , and
, and
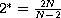 which is the critical Sobolev exponent.
which is the critical Sobolev exponent.
Yasmina Nasri
Abstract:
We prove the existence of nontrivial solutions for the singular critical
problem
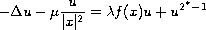
with Dirichlet boundary conditions. Here the domain is a smooth bounded
subset of
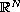 ,
,
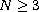 , and
, and
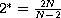 which is the critical Sobolev exponent.
which is the critical Sobolev exponent.
Submitted February 6, 2007. Published June 6, 2007.
Math Subject Classifications: 35J20, 35J60.
Key Words: Palais-Smale condition; singular potential; Sobolev exponent;
mountain-pass theorem.
Show me the PDF file (207K), TEX file for this article.
| Yasmina Nasri Université de Tlemcen, département de mathématiques BP 119 Tlemcen 13000, Algérie email: y_nasri@mail.univ-tlemcen.dz |
Return to the EJDE web page