We establish an integral representation for the Frobenius solution with an exponent zero at
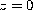of the general Heun equation.
First we present an extension of Mellin's lemma which provides
a powerful method that takes into account differential equations
which are not of the form studied by Mellin. That is the case
for equations of Heun's type.
It is that aspect which makes our work different from Valent's work.
The method is powerful because it allows obtaining directly the nucleus
equation of the representation. The integral representation formula
obtained with this method leads quickly and naturally to already known
results in the case of hypergeometric functions.
The generalisation of this method gives a type of differential equations
which form is a novelty and deserves to be studied further.
