Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 96, pp. 1-10.
Positive solutions for classes of multiparameter
elliptic semipositone problems
Scott Caldwell, Alfonso Castro,
Ratnasingham Shivaji, Sumalee Unsurangsie
Abstract:
We study positive solutions to multiparameter
boundary-value problems of the form
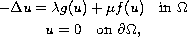
where
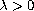 ,
,
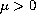 ,
,
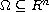 ;
;
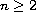 is a smooth bounded domain with
is a smooth bounded domain with
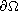 in class
in class
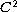 and
and
 is the Laplacian operator. In particular, we assume
is the Laplacian operator. In particular, we assume
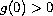 and superlinear while
and superlinear while
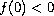 ,
sublinear, and eventually
strictly positive. For fixed
,
sublinear, and eventually
strictly positive. For fixed
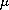 , we establish existence and
multiplicity for
, we establish existence and
multiplicity for
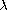 small, and nonexistence for
small, and nonexistence for
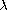 large. Our proofs are based on variational methods, the Mountain Pass
Lemma, and sub-super solutions.
large. Our proofs are based on variational methods, the Mountain Pass
Lemma, and sub-super solutions.
Submitted November 13, 2006. Published June 29, 2007.
Math Subject Classifications: 35J20, 35J65.
Key Words: Positive solutions; multiparameters; mountain pass lemma;
sub-super solutions; semipositone.
Show me the
PDF file (226 KB),
TEX file for this article.
 |
Scott Caldwell
Department of Mathematics and Statistics
Mississippi State University
Mississippi State, MS 39762, USA
email: pscaldwell@yahoo.com |
|---|
 |
Alfonso Castro
Department of Mathematics
Harvey Mudd College
Claremont, CA 91711, USA
email: castro@math.hmc.edu |
 |
R. Shivaji
Department of Mathematics and Statistics
Mississippi State University
Mississippi State, MS 39762, USA
e-mail: shivaji@math.msstate.edu |
| |
Sumalee Unsurangsie
Mahidol University, Thailand
|
|---|
Return to the EJDE web page
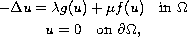
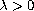 ,
,
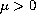 ,
,
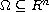 ;
;
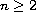 is a smooth bounded domain with
is a smooth bounded domain with
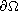 in class
in class
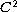 and
and
 is the Laplacian operator. In particular, we assume
is the Laplacian operator. In particular, we assume
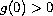 and superlinear while
and superlinear while
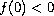 ,
sublinear, and eventually
strictly positive. For fixed
,
sublinear, and eventually
strictly positive. For fixed
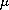 , we establish existence and
multiplicity for
, we establish existence and
multiplicity for
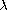 small, and nonexistence for
small, and nonexistence for
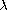 large. Our proofs are based on variational methods, the Mountain Pass
Lemma, and sub-super solutions.
large. Our proofs are based on variational methods, the Mountain Pass
Lemma, and sub-super solutions.


