Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 145, pp. 1-13.
Stability and approximations of eigenvalues and
eigenfunctions for the Neumann Laplacian, part I
Rodrigo Bañuelos, Michael M. H. Pang
Abstract:
We investigate stability and approximation properties of the lowest
nonzero eigenvalue and corresponding eigenfunction of the Neumann Laplacian
on domains satisfying a heat kernel bound condition.
The results and proofs in this paper will be used and extended
in a sequel paper to obtain stability results for domains in
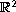 with a snowflake type boundary.
with a snowflake type boundary.
Submitted February 4, 2008. Published October 24, 2008.
Math Subject Classifications: 35P05, 35P15.
Key Words: Stability; approximations;
Neumann eigenvalues and eigenfunctions.
Show me the
PDF file (253 KB),
TEX file for this article.
| |
Rodrigo Bañuelos
Department of Mathematics, Purdue University
West Lafayette, IN 47906, USA
email: banuelos@math.purdue.edu
|
|---|
 |
Michael M. H. Pang
Department of Mathematics,
University of Missouri
Columbia, MO 65211, USA
email: pangm@math.missouri.edu
|
|---|
Return to the EJDE web page
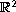 with a snowflake type boundary.
with a snowflake type boundary.
