Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 153, pp. 1-13.
Critical Neumann problem for nonlinear elliptic systems
in exterior domains
Shengbing Deng, Jianfu Yang
Abstract:
In this paper, we investigate the Neumann problem for a critical
elliptic system in exterior domains. Assuming
that the coefficient
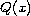 is a positive smooth function and
is a positive smooth function and
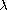 ,
,
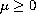 are parameters, we examine the common effect
of the mean curvature of the boundary
are parameters, we examine the common effect
of the mean curvature of the boundary
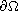 and the
shape of the graph of the coefficient
and the
shape of the graph of the coefficient
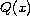 on the existence of the
least energy solutions.
on the existence of the
least energy solutions.
Submitted June 25, 2008. Published November 7, 2008.
Math Subject Classifications: 35J50, 35J60.
Key Words: Neumann problem; elliptic systems; exterior domains;
critical Sobolev exponent; least energy solutions.
Show me the
PDF file (249 KB),
TEX file for this article.
| |
Shengbing Deng
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: shbdeng@yahoo.com.cn
|
|---|
 |
Jianfu Yang
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
|---|
Return to the EJDE web page
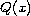 is a positive smooth function and
is a positive smooth function and
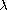 ,
,
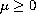 are parameters, we examine the common effect
of the mean curvature of the boundary
are parameters, we examine the common effect
of the mean curvature of the boundary
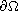 and the
shape of the graph of the coefficient
and the
shape of the graph of the coefficient
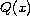 on the existence of the
least energy solutions.
on the existence of the
least energy solutions.
