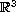 ,
Part 2: Nonconvex corners
,
Part 2: Nonconvex corners
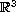 ,
Part 2: Nonconvex corners
,
Part 2: Nonconvex corners
Thalia Jeffres, Kirk Lancaster
Abstract:
The goal of this note is to continue the investigation started in
Part One of the structure of "blown up" sets of the form
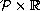 and
and
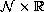 when
when
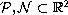 and
and
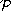 (or
(or
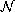 )
minimizes
an appropriate functional and the domain has a nonconvex corner.
Sets like
)
minimizes
an appropriate functional and the domain has a nonconvex corner.
Sets like
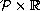 can be the limits of
the blow ups of subgraphs of solutions of capillary surface or
other prescribed mean curvature problems, for example. Danzhu Shi
recently proved that in a wedge domain
can be the limits of
the blow ups of subgraphs of solutions of capillary surface or
other prescribed mean curvature problems, for example. Danzhu Shi
recently proved that in a wedge domain
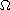 whose boundary
has a nonconvex corner at a point O and assuming the correctness
of the Concus-Finn Conjecture for contact angles 0 and
whose boundary
has a nonconvex corner at a point O and assuming the correctness
of the Concus-Finn Conjecture for contact angles 0 and
 , a
capillary surface in positive gravity in
, a
capillary surface in positive gravity in
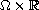 must be discontinuous under certain conditions. As an application,
we extend the conclusion of Shi's Theorem to the case where the
prescribed mean curvature is zero without any assumption about the
Concus-Finn Conjecture.
must be discontinuous under certain conditions. As an application,
we extend the conclusion of Shi's Theorem to the case where the
prescribed mean curvature is zero without any assumption about the
Concus-Finn Conjecture.
Submitted August 3, 2007. Published December 9, 2008.
Math Subject Classifications: 49Q20, 53A10, 76B45.
Key Words: Blow-up sets; capillary surface; Concus-Finn conjecture.
Show me the PDF file (364 KB), TEX file for this article.
 |
Thalia Jeffres Department of Mathematics and Statistics Wichita State University Wichita, Kansas, 67260-0033, USA email: jeffres@math.wichita.edu |
|---|---|
 |
Kirk Lancaster Department of Mathematics and Statistics Wichita State University Wichita, Kansas, 67260-0033, USA email: lancaster@math.wichita.edu |
Return to the EJDE web page