The asymptotic dynamics of high-order temporal-spatial derivatives of the two-dimensional vorticity and velocity of an incompressible, viscous fluid flow in
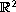 are studied,
which is equivalent to the 2D Navier-Stokes equation. It is known
that for any integrable initial vorticity, the 2D vorticity
solution converges to the Oseen vortex. In this paper, sharp
exterior decay estimates of the temporal-spatial derivatives of
the vorticity solution are established. These estimates are then
used and combined with similarity and
are studied,
which is equivalent to the 2D Navier-Stokes equation. It is known
that for any integrable initial vorticity, the 2D vorticity
solution converges to the Oseen vortex. In this paper, sharp
exterior decay estimates of the temporal-spatial derivatives of
the vorticity solution are established. These estimates are then
used and combined with similarity and
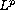 compactness to show
the asymptotical attraction rates of temporal-spatial derivatives
of generic 2D vorticity and velocity solutions by the Oseen
vortices and velocity solutions respectively. The asymptotic estimates
and the asymptotic attraction rates of all the derivatives obtained
in this paper are independent of low or high Reynolds numbers.
compactness to show
the asymptotical attraction rates of temporal-spatial derivatives
of generic 2D vorticity and velocity solutions by the Oseen
vortices and velocity solutions respectively. The asymptotic estimates
and the asymptotic attraction rates of all the derivatives obtained
in this paper are independent of low or high Reynolds numbers.
