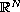Electron. J. Diff. Eqns., Vol. 2008(2008), No. 46, pp. 1-23.

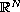Asymptotic behavior for a dissipative plate equation in $\mathbb{R}^N$ with periodic coefficients

Ruy C. Charao, Eleni Bisognin, Vanilde Bisognin, Ademir F. Pazoto

Abstract:
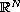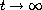In this work we study the asymptotic behavior of solutions of a dissipative plate equation in $\mathbb{R}^N$ with periodic coefficients. We use the Bloch waves decomposition and a convenient Lyapunov function to derive a complete asymptotic expansion of solutions as $t\to \infty$. In a first approximation, we prove that the solutions for the linear model behave as the homogenized heat kernel.

Submitted June 7, 2007. Published March 29, 2008.
Math Subject Classifications: 35C20, 35B40, 35B27, 35L15.
Key Words: Asymptotic behavior; homogenization; partial differential equations; media with periodic structure; second-order hyperbolic equations.

Show me the PDF file (355 KB), TEX file, and other files for this article.

  Ruy Coimbra Charão
Departamento de Matemática, Universidade Federal de Santa Catarina
P. O. Box 476, CEP 88040-900, Florianópolis, SC, Brasil
email: charao@mtm.ufsc.br
  Eleni Bisognin
Centro Universitário Franciscano
Campus Universitário, 97010-032, Santa Maria, RS, Brasil
email: eleni@unifra.br
  Vanilde Bisognin
Centro Universitário Franciscano
Campus Universitário, 97010-032, Santa Maria, RS, Brasil
email: vanilde@unifra.br
Ademir Fernando Pazoto
Instituto de Matemática, Universidade Federal do Rio de Janeiro
P. O. Box 68530, CEP 21945-970, Rio de Janeiro, RJ, Brasil
email: ademir@acd.ufrj.br

Return to the EJDE web page