Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 54, pp. 1-6.
Liapunov exponents for higher-order linear
differential equations whose characteristic equations have
variable real roots
Michael I. Gil'
Abstract:
We consider the linear differential equation
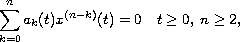
where
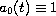 ,
,
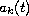 are continuous bounded functions.
Assuming that all the roots of the polynomial
are continuous bounded functions.
Assuming that all the roots of the polynomial
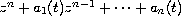 are real and satisfy the inequality
are real and satisfy the inequality
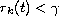 for
for
 and
and
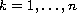 ,
we prove that the solutions of the above equation satisfy
,
we prove that the solutions of the above equation satisfy
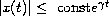 for
for
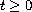 .
.
Submitted December 27, 2007. Published April 15, 2008.
Math Subject Classifications: 34A30, 34D20.
Key Words: Linear differential equations; Liapunov exponents;
exponential stability.
Show me the
PDF file (192 KB),
TEX file for this article.
 |
Michael I. Gil'
Department of Mathematics
Ben Gurion University of the Negev
P.0. Box 653, Beer-Sheva 84105, Israel
Email: gilmi@cs.bgu.ac.il |
|---|
Return to the EJDE web page
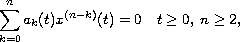
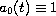 ,
,
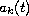 are continuous bounded functions.
Assuming that all the roots of the polynomial
are continuous bounded functions.
Assuming that all the roots of the polynomial
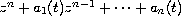 are real and satisfy the inequality
are real and satisfy the inequality
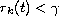 for
for
 and
and
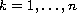 ,
we prove that the solutions of the above equation satisfy
,
we prove that the solutions of the above equation satisfy
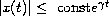 for
for
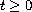 .
.
