Electron. J. Diff. Eqns.,
Vol. 2008(2008), No. 98, pp. 1-10.
Existence of solutions for a resonant problem under
Landesman-Lazer conditions
Quoc Anh Ngo, Hoang Quoc Toan
Abstract:
This article shows the existence of weak solutions in
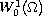 to a class of Dirichlet problems of the form
to a class of Dirichlet problems of the form
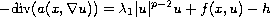
in a bounded domain
 of
of
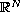 .
Here a satisfies
.
Here a satisfies
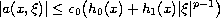
for all
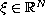 ,
a.e.
,
a.e.
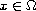 ,
,
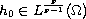 ,
,
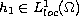 ,
,
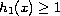 for a.e. x in
for a.e. x in
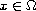 ;
;
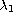 is the first eigenvalue for
is the first eigenvalue for
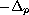 on
on
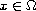 with zero Dirichlet
boundary condition and g, h satisfy some suitable conditions.
with zero Dirichlet
boundary condition and g, h satisfy some suitable conditions.
Submitted March 24, 2008. Published July 25, 2008.
Math Subject Classifications: 35J20, 35J60, 58E05.
Key Words: p-Laplacian; Non-uniform; Landesman-Laser type;
Divergence form.
Show me the
PDF file (235 KB),
TEX file for this article.
 |
Quocc Anh Ngo
Department of Mathematics,
College of Science
Vietnam National University, Hanoi, Vietnam
email: bookworm_vn@yahoo.com, nqanh@vnu.edu.vn
|
|---|
 |
Hoang Quoc Toan
Department of Mathematics,
College of Science
Vietnam National University, Hanoi, Vietnam
email: hq_toan@yahoo.com
|
|---|
Return to the EJDE web page
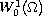 to a class of Dirichlet problems of the form
to a class of Dirichlet problems of the form
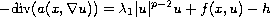
 of
of
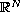 .
Here a satisfies
.
Here a satisfies
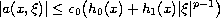
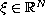 ,
a.e.
,
a.e.
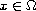 ,
,
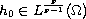 ,
,
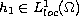 ,
,
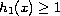 for a.e. x in
for a.e. x in
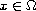 ;
;
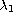 is the first eigenvalue for
is the first eigenvalue for
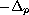 on
on
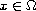 with zero Dirichlet
boundary condition and g, h satisfy some suitable conditions.
with zero Dirichlet
boundary condition and g, h satisfy some suitable conditions.

