Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 02, pp. 1-11.
Nonexistence results for semilinear systems in unbounded domains
Brahim Khodja, Abdelkrim Moussaoui
Abstract:
This paper concerns the non-existence of nontrivial solutions for the
semi-linear system of gradient type
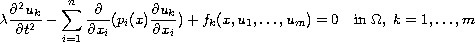
with Dirichlet, Neumann or Robin boundary conditions. The functions
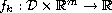
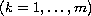 are locally Lipschitz continuous and satisfy
are locally Lipschitz continuous and satisfy
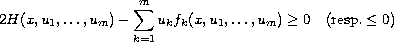
for
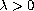 (resp.
(resp.
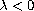 ).
We establish the non-existence of
nontrivial solutions using Pohozaev-type identities.
Here
).
We establish the non-existence of
nontrivial solutions using Pohozaev-type identities.
Here
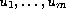 are in
are in
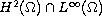 ,
,
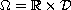 with
with
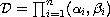 and
and
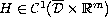 such that
such that
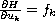 ,
,
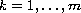 .
.
Submitted April 10, 2008. Published January 2, 2009.
Math Subject Classifications: 35J45, 35J55.
Key Words: Semi linear systems; Pohozaev identity; trivial solution;
Robin boundary condition.
Show me the PDF file (247 KB),
TEX file for this article.
 |
Brahim Khodja
Department of mathematics, Badji Mokhtar University
B.P. 12 Annaba, Algeria
email: bmkhodja@yahoo.fr
|
|---|
 |
Abdelkrim Moussaoui
Department of mathematics, Badji Mokhtar University
B.P. 12 Annaba, Algeria
email: remdz@yahoo.fr
|
|---|
Return to the EJDE web page
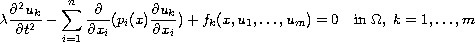
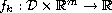
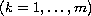 are locally Lipschitz continuous and satisfy
are locally Lipschitz continuous and satisfy
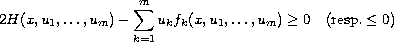
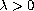 (resp.
(resp.
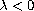 ).
We establish the non-existence of
nontrivial solutions using Pohozaev-type identities.
Here
).
We establish the non-existence of
nontrivial solutions using Pohozaev-type identities.
Here
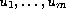 are in
are in
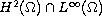 ,
,
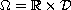 with
with
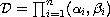 and
and
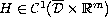 such that
such that
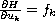 ,
,
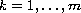 .
.

