Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 107, pp. 1-11.
Inverse eigenvalue problems for
semilinear elliptic equations
Tetsutaro Shibata
Abstract:
We consider the inverse nonlinear eigenvalue problem for
the equation
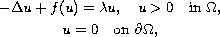
where
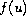 is an unknown nonlinear term,
is an unknown nonlinear term,
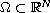 is a bounded domain with an
appropriate smooth boundary
is a bounded domain with an
appropriate smooth boundary
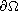 and
and
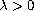 is a parameter.
Under basic conditions on
is a parameter.
Under basic conditions on
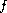 , for any given
, for any given
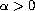 ,
there exists a unique solution
,
there exists a unique solution
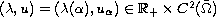 with
with
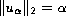 .
The curve
.
The curve
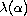 is called the
is called the
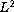 -bifurcation
branch. Using a variational approach, we show that the
nonlinear term
-bifurcation
branch. Using a variational approach, we show that the
nonlinear term
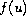 is determined uniquely by
is determined uniquely by
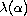 .
.
Submitted November 14, 2008. Published September 10, 2009.
Math Subject Classifications: 35P30.
Key Words: Inverse eigenvalue problems; nonlinear elliptic equation;
variational method.
Show me the PDF file (243 KB),
TEX file for this article.
 |
Tetsutaro Shibata
Department of Applied Mathematics
Graduate School of Engineering
Hiroshima University, Higashi-Hiroshima, 739-8527, Japan
email: shibata@amath.hiroshima-u.ac.jp
|
|---|
Return to the EJDE web page
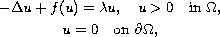
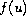 is an unknown nonlinear term,
is an unknown nonlinear term,
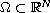 is a bounded domain with an
appropriate smooth boundary
is a bounded domain with an
appropriate smooth boundary
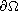 and
and
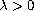 is a parameter.
Under basic conditions on
is a parameter.
Under basic conditions on
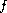 , for any given
, for any given
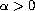 ,
there exists a unique solution
,
there exists a unique solution
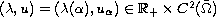 with
with
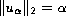 .
The curve
.
The curve
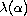 is called the
is called the
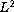 -bifurcation
branch. Using a variational approach, we show that the
nonlinear term
-bifurcation
branch. Using a variational approach, we show that the
nonlinear term
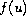 is determined uniquely by
is determined uniquely by
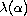 .
.
