Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 124, pp. 1-18.
Infinite multiplicity of positive solutions for singular
nonlinear elliptic equations with convection term and
related supercritical problems
Carlos C. Aranda
Abstract:
In this article, we consider the singular nonlinear elliptic problem
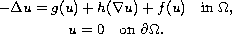
Under suitable assumptions on
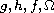 that allow a singularity of g at the origin, we obtain
infinite multiplicity results. Moreover, we state infinite
multiplicity results for related boundary blow up supercritical
problems and for supercritical elliptic problems
with Dirichlet boundary condition.
that allow a singularity of g at the origin, we obtain
infinite multiplicity results. Moreover, we state infinite
multiplicity results for related boundary blow up supercritical
problems and for supercritical elliptic problems
with Dirichlet boundary condition.
Submitted August 24, 2009. Published October 1, 2009.
Math Subject Classifications: 35J25, 35J60.
Key Words: Bifurcation; degree theory; nonlinear eigenvalues
and eigenfunctions.
Show me the PDF file (287 KB),
TEX file for this article.
 |
Carlos C. Aranda
Laboratorio de modelización, cálculo numérico y
diseno experimental
Facultad de Recursos Naturales
Universidad Nacional de Formosa,
Argentina
email: carloscesar.aranda@gmail.com
|
|---|
Return to the EJDE web page
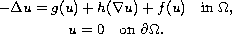
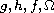 that allow a singularity of g at the origin, we obtain
infinite multiplicity results. Moreover, we state infinite
multiplicity results for related boundary blow up supercritical
problems and for supercritical elliptic problems
with Dirichlet boundary condition.
that allow a singularity of g at the origin, we obtain
infinite multiplicity results. Moreover, we state infinite
multiplicity results for related boundary blow up supercritical
problems and for supercritical elliptic problems
with Dirichlet boundary condition.
